I. Alapjelenség: a mozgó testek eltérülése
Otthon is elvégezheted a következő egyszerű kísérletet egy papírkorong, ceruza és vonalzó segítségével: A papírkorongot a középpontjába szúrt rajzszöggel rögzítsd egy deszkához. Állandó sebességgel mozgó ceruzával először a nyugvó korongra rajzolj egy egyenes vonalat, a középpontból kiindulva. Ezután ismételd meg ugyanezt a mozgást úgy, hogy miközben húzod a vonalat, valaki nagyjából egyenletes szögsebességgel forgatja a korongot az óra járásának irányában, ahogyan ezen a felvételen is látható: video4. Ezúttal görbe vonalat fogsz kapni, a ceruza pályája eltérül az egyenestől, mint itt.
Jól látható, hogy a körhintán mozgó test (csakúgy, mint a ceruzavonal a forgó papírkorongon) eltérül az eredeti irányától. Figyeld meg, hogy bal felé térül el, ha a forgás az óramutató irányában történik. Ugyanaz az eltérülés tapasztalható a videókon látható elgurított labda (video2), illetve ceruzavonal (video4) esetében.
Megjegyzés: a nem forgó papírkorong egyenes vonala felel meg a nyugvó vonatkoztatási rendszerből megfigyelt egyenletes mozgásnak. Az eltérülés tehát annak a következménye, hogy ezt az egyébként egyszerű mozgást forgó vonatkoztatási rendszerből figyeljük meg.
A forgó korongon megjelenő ceruzavonal parabolára emlékeztet, legalábbis kicsi elmozdulások esetében. Ez arra utal, hogy a körhintához viszonyított mozgás hasonlít az állandó gyorsulással történő mozgáshoz.
A kísérletben rajzolt görbe vonalnak tekintsd azt a részét, amely rövid idejű mozgásnak felel meg (vagyis a görbének a kezdőponthoz közeli szakaszát). Ennek néhány pontjában mérd meg az egyenes vonaltól való eltérülést.
1. Az egyenes mentén való elmozdulást feleltesd meg az eltelt időnek (önkényes egységekben), és mutasd meg, hogy az összefüggés (legalábbis rövid idők esetén) valóban parabolikus, majd határozd meg a gyorsulást.
2. Tudjuk, hogy a középponttól $r$ távolságra levő pont $r \Omega t$ hosszúságú körívet ír le, ahol $\Omega$ a papírkorong forgásának szögsebessége. Ezt felhasználva fejezd ki a gyorsulást az $\Omega$ szögsebességgel és a ceruza mozgatásának $v$ sebességével. Írd fel azt az az erőt is, amely ekkora gyorsulást hoz létre.
Az eltérülésnek megfeleltethető erő a Coriolis-erő. Nagysága $$ {F_C=m 2 v \Omega}, $$ iránya pedig a $\boldsymbol{v}$ sebesség irányára merőleges, és a mozgásirányhoz képest balra, illetve jobbra mutat, amikor a forgás az óra járásának irányában, illetve azzal ellentétesen történik.
3.
Hogy alaposabban megértsd a jelenséget,
végezz el egy valamivel bonyolultabb kísérletet: Ismételd meg az előző kísérletet úgy, hogy a ceruzavonalat a forgástengelytől
$r_0$ távolságban indítod, sugárirányban kifelé: video5. Vajon ezúttal más kifejezés adódik a
gyorsulásra, illetve az erőre, amely a sebesség irányára merőlegesen hat?
Az erő most is $F_C=m 2 v \Omega$, de $v$ itt már a testnek a forgó vonatkoztatási rendszerhez viszonyított sebességét jelenti. Megjelenik továbbá egy újabb, sugárirányban kifelé ható erő is, ez a $F_{cf}=m r_0 \Omega^2$ centrifugális erő. Mindkét erő befolyásolja a körhintán elindított labda mozgását, de csak a Coriolis-erő felelős a sebesség eredeti irányától való eltérülésért.
Egy alapvető kvantitatív mérőszám: az eltérülés erőssége
Tekintsünk egy testet, amelynek a nemforgó vonatkoztatási rendszerből nézve $U$ lenne a sebessége, és becsüljük meg, hogy e kezdősebesség irányától mérve mekkora $D$ eltérülést okoz a Coriolis-erő, mialatt a test $L$ távolságba jut.
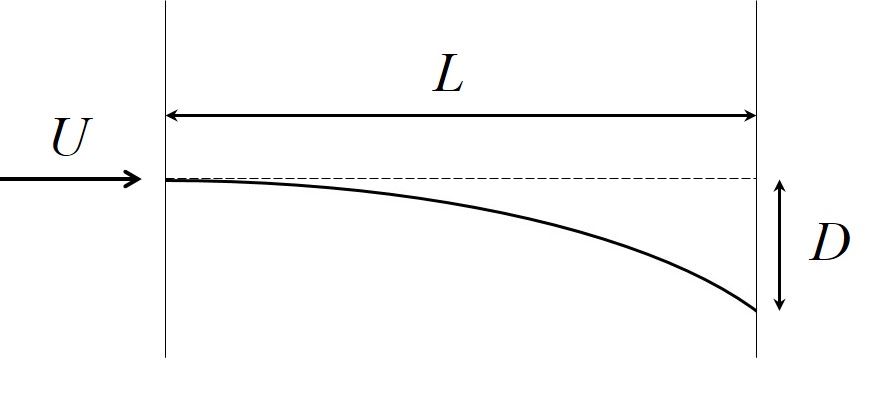
Tételezzük fel, hogy az eltérülés az $L$ távolsághoz képest igen kicsi ($D \ll L)$. Ekkor a $2 v \Omega$ gyorsulás állandónak tekinthető, és nagysága közelítőleg $2 U \Omega$. Ezzel a közelítéssel a sebesség kezdeti irányára merőlegesen történő $D$ eltérülés nagysága $t$ idő elteltével $(1/2)a_C t^2$, azaz $(1/2) 2 U \Omega t^2$. Az $L$ távolság megtételéhez szükséges idő körülbelül $L/U$, így $$D=U \Omega L^2 /U^2 = \Omega L^2 /U.$$ Érdemes vizsgálni a relatív eltérülést is, vagyis a $D$ távolságnak a teljes $L$ távolsághoz viszonyított $D/L$ arányát: $$ \boxed{D/L = \Omega L/U.} $$ Ez az egyszerű kifejezés jól alkalmazható a Coriolis-hatás miatti eltérülés erősségének becslésére. Általános esetben a mozgás átlagos sebességét tekintjük $U$ értékének. A relatív eltérülés $D/L=\Omega L/U$ kifejezését általános esetben is az eltérülés erősségét megadó kvantitatív mérőszámnak tekintik. Vegyük észre, hogy ez a mérőszám fordítottan arányos $U$ értékével, hiszen az eltérülést nemcsak a gyorsulás határozza meg, hanem az is, hogy mennyi ideig hat a Coriolis-erő.
