A körhintától a ciklonokig és a Golf-áramlatig

III. Erős Coriolis-eltérülés

Az eltérítő hatás lényeges tulajdonsága, hogy földrajzi méretskálákon az eltérülés már igen erős lehet. Az I. szakaszban $D$ értékére adott becslésünk már nem érvényes, amikor a $D$ eltérülés nem sokkal kisebb az $L$ térbeli kiterjedésnél. Az $$ \boxed{S=\Omega_V L /U} $$ arány azonban (ahol a körhinta esetében $\Omega_V$ helyett $\Omega$ írandó), ilyenkor is jó mérőszámként jellemzi az $U$ tipikus sebességű mozgás Coriolis-eltérülésének erősségét (bár $S \neq D/L$). Ha ez az arány egység nagyságrendű, akkor tudjuk, hogy az eltérülés összemérhető a teljes elmozdulással. Az eltérítő hatás tehát erősnek bizonyul, ha ez az arány 1-nél nagyobb.

13. Becsüld meg az eltérülés $S$ erősségét a) a papírkorongos kísérletben, illetve b) a körhintás videóban (video2), ahol a tipikus hosszúságskálák $L=10$ cm, illetve $L=1$ m. A többi tipikus számérték (lásd a 2a feladat megoldását) legyen az a) esetben $\Omega=\pi/10$ 1/s és $U=2$ cm/s, a b) esetben pedig $\Omega=\pi$ 1/s és $U=0,5$ m/s .

Az $S=\Omega L /U$ arány értéke $\pi/2=1,6$ az a) feladatban, és $2 \pi=6,3$ a b) feladatban. Az, hogy erősnek tekintjük az eltérülést, amikor az arány 1-nél nagyobb, összhangban van mind a körhintás videóval (hiszen az eltérítés hatására a labda visszatérhet az indítási helyre), mind pedig a papírkorongos kísérlettel (hiszen ha nem lenne erős, akkor a két ceruzavonalat nagyon nehéz lenne megkülönböztetni egymástól). Vegyük észre, hogy csakis a Coriolis-gyorsulás ismeretében még nem tudnánk megállapítani, hogy az eltérülés mindkét esetben erős (lásd a 2a feladat megoldását).

14.Tekintsük azt az esetet, amikor a körhintás videóban a labdát elgurító gyerekhez visszatér a labda. Tegyük fel, hogy (elhanyagolható súrlódás mellett) a labda pályája áthalad a körhinta középpontján. Ha a gyerek $r$ távolságra helyezkedik el a középponttól és a szögsebesség $\Omega$, mekkora (és milyen irányú) legyen a labda kezdeti, érintőirányú sebessége a körhintához képest, hogy ilyen mozgás jöjjön létre? Hogyan kell megválasztani a labda sugárirányú sebességét, hogy a labda éppen egy fél körhintafordulat múlva érkezzen vissza?

A labdának adott érintőirányú sebesség egyenlő nagyságú és ellentétes irányú kell, hogy legyen a körhinta kerületi sebességével: $r \Omega$ jobb felé. Az álló megfigyelő azt látja, hogy a labda egyenletes $v$ sebességgel végighalad egy $2r$ átmérő mentén $t=2r/v$ idő alatt. Ez akkor történik épp egy fél fordulat alatt, ha $t=\pi/\Omega$, ahonnan $v=2 r \Omega/\pi $.

Az erősség $S$ kifejezésének figyelemreméltó tulajdonsága, hogy növekszik a távolsággal. Adott sebesség esetén minél nagyobb a mozgás térbeli kiterjedése, annál erősebb az effektus. Ez az oka annak, hogy bár a Föld lassan forog a tengelye körül, mégis erős eltérüléseket figyelhetünk meg nagy, földrajzi méretskálákon. A légkör és az óceánok nagyléptékű mozgásaiban a Coriolis-eltérülést sosem lehet figyelmen kívül hagyni. Sőt, a Coriolis-erő majd minden egyéb erőnél nagyobbá válik.

15. Becsüld meg az eltérülés $S$ erősségét a forgó Földön, közepes szélességen a) egy $L=1000 \text{ km}$ méretű ciklonban, ahol a szél $U=10 \text{ m/s}$ sebességgel fúj, illetve b) egy $L=100 \text{ km}$ sugarú óceáni örvényben, ahol a víz sebessége $U=1 \text{ m/s}$.

Az $S=\Omega_V L /U$ hányados értéke $5 \cdot 10^{-5} \cdot 10^6/10=5$ a ciklonban (a), és $5 \cdot 10^{-5} \cdot 10^5/1=5$ az óceáni örvényben (b). A kapott eredmények egyenlősége jelzi, hogy a Coriolis-erő a légkörben és az óceánban egyformán jelentős szerepet játszik.

A ciklonok mint légköri felfolyók

Ismert, hogy a mérsékeltövi ciklonok esőt hoznak. Ennek az a magyarázata, hogy a ciklon közepén alacsony a nyomás (L), és ennek hatására a felszínről nedves levegő emelkedik fel, ami csapadékképződéshez vezet.

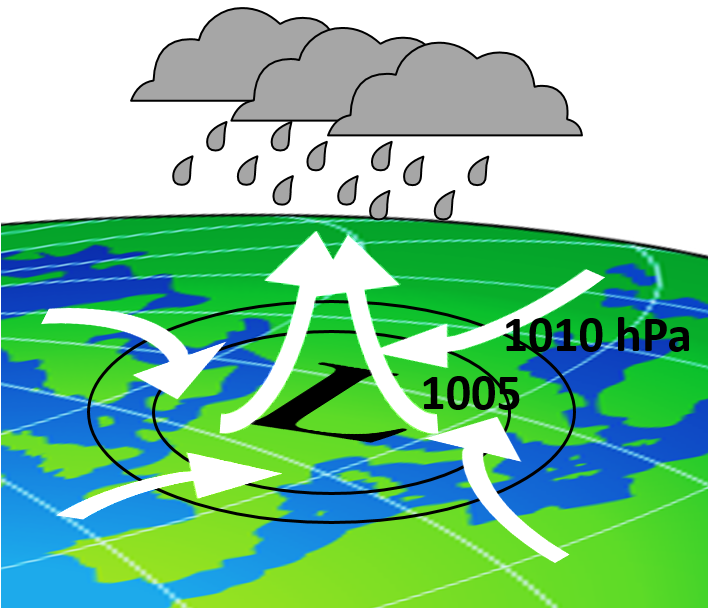
A feláramlás csak úgy lehetséges, ha az alacsonyabb légrétegekben a középpont felé irányuló áramlás történik. A fürdőkádban lefolyó víz tárgyalásakor rajzolt

ábra tehát a ciklon közepe felé áramló levegő esetében tökéletesen helytálló. A Coriolis-effektus révén az Északi-féltekén a befelé áramló levegőrészek elkanyarodnak jobb felé (a Déli-féltekén bal felé). Az így létrejövő hatalmas levegőörvény az óramutató járásával ellentétes irányban forog (a Déli-féltekén pedig az óramutató irányában). Olyan, mint egy gigantikus fejreállított lefolyó.

Anglia felé közeledő ciklon, 2012. augusztus

Ciklon Nyugat-Ausztrália fölött, 2004. március

Minden ciklon kivétel nélkül így viselkedik! Ennek oka, hogy amint láttuk, szinte nincs is olyan hatás, amely nagy méretskálákon a Coriolis-hatással vetekedne. Ami észrevehetetlen volt az otthoni lefolyóban, az nap, mint nap erőteljesen jelen van a ciklonok által uralt időjárás-előrejelzéseinkben. A ciklonok mindig úgy forognak, ahogyan a Coriolis-erő diktálja. (Természetesen az anticiklonok is forognak,a ciklonokkal ellentétesen, de — mivel nincsenek felhők, amelyek kirajzolnák a spirális szerkezetet — nem látszanak olyan jól az időjárási térképeken.) Az Egyenlítőnél $\Omega_V$ eltűnik, így eltérítő hatás hiányában nem léteznek ciklonok sem! (Tudni kell, hogy a trópusi ciklonnak is nevezett hurrikánok nem egyenlítői ciklonok: csak minimum 15 fokos északi vagy déli szélességen fordulnak elő.) Hogyan is okozhatná a Coriolis-hatás a legelső videón látott lefolyó örvénylését! Ez a megtévesztő videó az interneten fellelhető számos másik videóval együtt szándékos félrevezetés.

A levegő nem arra mozog, amerre a nyomás hajtja, hanem rá merőlegesen

Egyetlen erő létezik, amely nagy méretskálákon a Coriolis-erő vízszintes komponensével összemérhető, mégpedig a vízszintes nyomáskülönbségekből származó erő. Ez az erő a magasabbtól az alacsonyabb nyomás felé hajtaná az anyagot. Az áramló légtömegek (vagy folyadék) gyorsulását az eredő erő határozza meg. Mivel a légkörben és az óceánban a sebesség változásai igen lassúak, a gyorsulás gyakorlatilag elhanyagolható. Ennek megfelelően a $\boldsymbol{F}_C$ Coriolis-erő, valamint a vízszintes nyomáskülönbségekből származó $\boldsymbol{F}$ erő kiegyenlíti egymást. Az $\boldsymbol{F}_C$ és $\boldsymbol{F}$ vektorok egymás ellentettjei, ahogyan az Északi-féltekére vonatkozó ábra mutatja (az egyenes vonalak az állandó nyomás görbéit, azaz az izobárokat jelképezik, és $\boldsymbol{F}$ a magas nyomástól az alacsony felé mutat.)

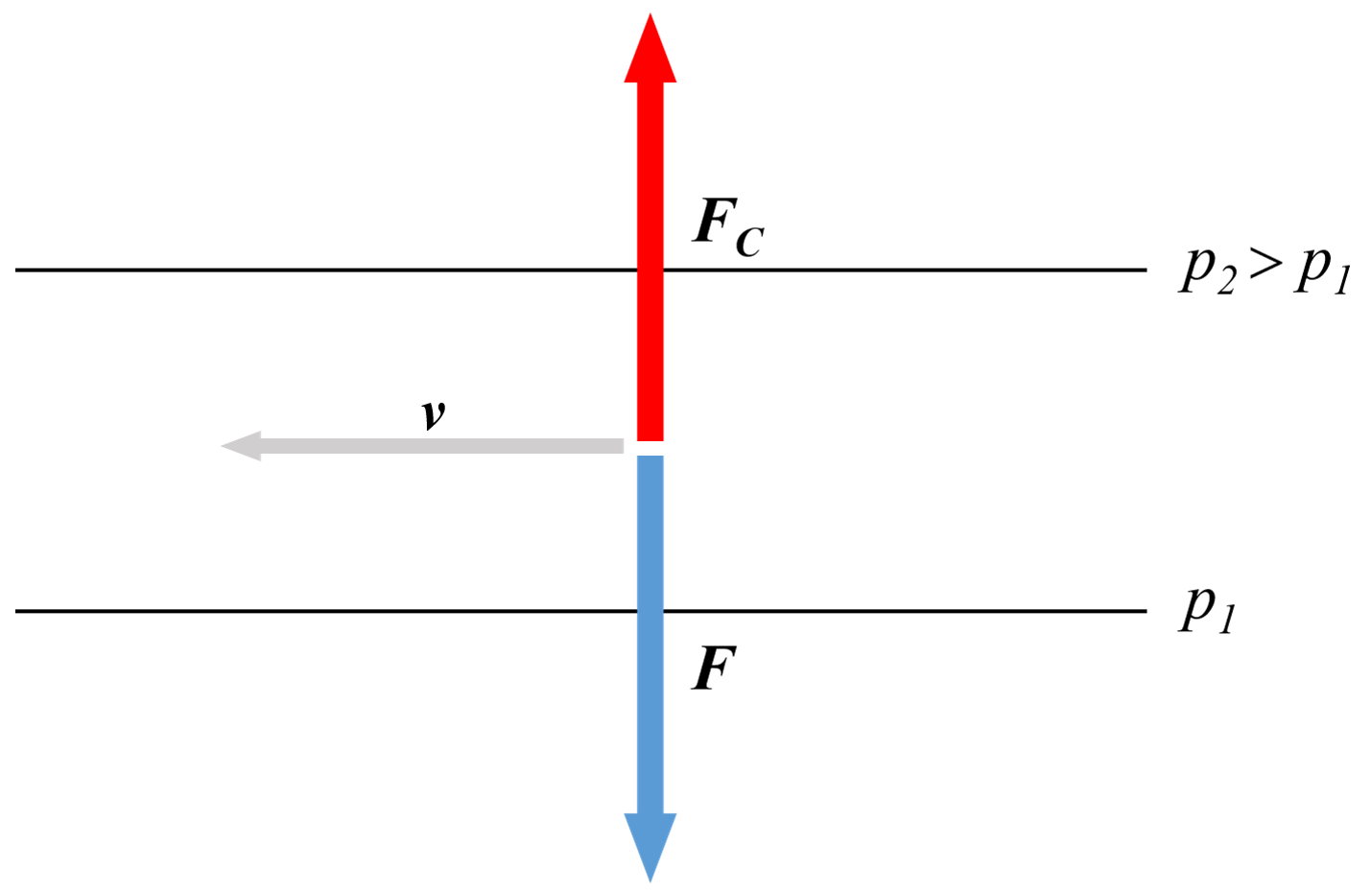
A $\boldsymbol{v}$ sebességvektor azonban merőleges a Coriolis-erőre, ezért a sebesség szükségképpen merőleges a nyomási erőre is. Így a levegő- vagy víztömegek nem abban az irányban mozognak, amerre a nyomás hajtja őket, hanem a nyomáskülönbségek irányára merőlegesen. Ez ellentétes a hétköznapi tapasztalatainkkal: egy csőben áramló gáz vagy folyadék mindig arra mozdul el, amerre a nyomás hajtja. Nem csoda, hiszen kis méretskálákon a Coriolis-erő nagyon gyenge.

A hajtóerőre merőleges irányban történő mozgást a körhintán guruló golyó esetében is megfigyelhetjük egy egyszerű kísérlettel. Vegyünk egy kis hajlásszögű lejtőt, és engedjük el rajta a golyót kezdősebesség nélkül. Kezdetben a golyót csak a nehézségi erő hajtja (ez felel meg most a nyomási erőnek), és a golyó elindul lefelé a lejtőn. Ahogy nő a sebessége, egyre nagyobb a rá ható Coriolis-erő, és létrejön egy spirál-szerű pálya, ahol az eredő elmozdulás lényegében vízszintes, vagyis a hajtóerőre merőleges. Az itt látható kísérletben a lejtő a kép alja felé lejt: video7 .

Időjárási térképek

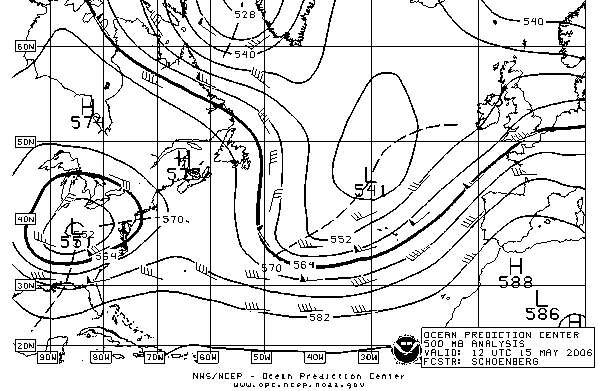
A sebesség és a nyomási erő merőlegességének meglepő következménye, hogy az időjárási térképek izobárjai, azaz az állandó nyomás görbéi a nyilakkal jelölt széliránnyal párhuzamosan futnak. Az Északi-féltekén a magas nyomás a nyilak irányától jobbra található. Történeti előzmény: Buys Ballot széltörvénye.

Buys Ballot-féle széltörvény

Az Északi-féltekén fújó szelekről Buys Ballot holland meteorológus az alábbi szabályt állapította meg 1857-ben: ha háttal állunk a szélnek, akkor az alacsonyabb nyomás mindig tőlünk balra található.

Az ábra bal oldalán, illetve középtájt egy-egy ciklon látható: az izobárok zárt görbék, belül vannak a legalacsonyabb nyomásértékek (L), és a szél az óra járásával ellentétes irányban fúj.

Keress az interneten hasonló nyomástérképeket, amelyek a mostani időjárást mutatják.

Az óceáni áramlatok felett lejt a vízfelszín

Az óceáni áramlatok esetében a Coriolis-erő és a nyomási erő egyensúlyának meglepő következménye, hogy az áramlatok felett a vízfelszín nem vízszintes, hanem oldalirányban kissé lejt. Ennek az a magyarázata, hogy lassú áramlások esetén egy adott mélységben uralkodó nyomás gyakorlatilag azonos a hidrosztatikai nyomással, amely pedig a vízoszlop magasságával arányos. A vízszintes nyomáskülönbség ezért magasságkülönbséggel jár. Az Északi-féltekén haladó óceáni áramlatok jobb oldalán a vízfelszínnek így magasabbnak kell lennie, mint a bal oldalon.

Az ábra a Golf-áramlat feletti tengerfelszín magasságát mutatja átlagolva (egy hónapra, hogy a hullámzás okozta eltérések kiegyenlítődjenek). A nyilak a sebességeket ábrázolják, míg a színek jelenítik meg a tengerfelszín magasságát egy vonatkoztatási szinthez képest (az átlagos tengerszinthez képest, cm-ben kifejezve). A Golf-áramlattól (ahol a nyilak a leghosszabbak) jobbra a felszín magassága $60$ cm, balra pedig $-40$ cm. A körülbelül $100$ km széles áramlat feletti teljes szintkülönbség tehát 1 méter. Az ábrán jól kivehető néhány narancssárga folt a piros tartomány belsejében. Ezek az óra járásával ellentétes irányú örvények, hiszen a belsejükben nyomásminimum található.

16. A fenti megfigyelések matematikai összefüggések formájában is kifejezhetők. Az itt bemutatott összefüggések alkalmazásával becsüld meg a légköri és óceáni mozgásokat jellemző sebességeket!

A természetben előforduló erős Coriolis-eltérülést szemléltető laboratóriumi kísérletek forgó folyadékokkal

Láttuk, hogy az otthoni lefolyókban az eltérülés erőssége $10^{-4}$ nagyságrendű. Az alacsony érték a Föld forgásának lassúságára vezethető vissza: mindössze 1 fordulat egy teljes nap alatt. Körülbelül 10 000-szer ilyen gyorsan forgó laboratóriumi eszközökkel azonban erős eltérülés is megvalósítható. Ekkora forgatási sebesség nem jelent nehézséget: mivel egy nap 1440 percből áll, csak percenként néhány fordulatra van szükség (ami sokkal lassabb egy CD-lejátszó forgásánál). Sőt, a paraméterek megfelelő megválasztása mellett a forgó tartályokkal végzett kísérletek nemcsak az erős eltérülés bemutatására alkalmasak, de valósághűen szemléltetik a légkör és az óceán nagyskálájú áramlásainak lényeges vonásait.

17. Mutasd meg, hogy ha a forgó tartály percenként 5 fordulatot tesz meg, és benne $U=1 \text{ cm/s}$ sebességű folyadékmozgás hatására $L=10$ cm méretű mintázat figyelhető meg, akkor az eltérülés $S$ erőssége pontosan ugyanakkora, mint a ciklonokban vagy az óceáni örvényekben.

Ebben az esetben a forgás periódusideje $T=12$ s. A szögsebesség $\Omega = 2 \pi/T \approx 0.5$ 1/s. Az $S=\Omega L /U$ hányados értéke tehát $0,5 \cdot 0,1/0,01=5$.

Hogy lássuk milyen jól utánozza a tartály a természetet, vegyünk egy $25$ cm sugarú hengert, töltsük meg vízzel $10$ cm magasságig, és forgassuk percenként néhány fordulattal. Hirtelen felülről fecskendezzünk festéket a tartályba. Amikor a festék néhány cm mélységbe lejut, érdekes mintázat alakul ki, ahogyan a következő videóban is látható: video8.

Festékfüggöny kialakulását figyelhetjük meg. (Az álló folyadékban ilyen nincs!) A festékrészecskék minden magasságban ugyanúgy mozognak, ami abból következik, hogy a Coriolis-eltérülés csak a festék vízszintes sebességétől függ (ez pedig a befecskendezés utáni pillanatban és ezt követően továbbra is mindig minden festékrészecskére ugyanaz), tehát nem függ a magasságtól. A festékfüggöny sokáig fennmarad, és (felülről nézve) hullámossá válik az egymás mellett sorban kialakuló örvények hatására, amelyek a ciklonokkal, illetve anticiklonokkal analóg módon az óra járásával ellenkezően, illetve annak megfelelően forognak. A mintázat nagyon hasonló a sarki fény (Aurora Borealis) esetében látott mintázatokhoz.

Ez nem véletlen: a fényt kibocsátó molekulák is az erős Coriolis-eltérítés hatására mozognak így a sztratoszférában. Más hasonló kísérletekről itt és itt olvashatsz.

Megfelelően tervezett forgótartályos kísérletekkel modellezni lehet a légköri cirkuláció lényeges vonásait, köztük az egyenlítői és a sarki régiók közötti hőmérsékletkülönbség csökkenése nyomán létrejövő változásokat (vagyis a klímaváltozás jelenségét) is.

Ellenőrző kérdéssor III