Feature 2, unpredictability
An additional characteristic feature of chaos shows up when comparing motions initiated with nearly identical conditions. In the first experiment this can be demonstrated by fixing two rulers to the same periodically moving axis, so that the rulers can move in two parallel planes without collisions. The rulers are practically identical (are made by the same producer).
Do you expect any essential deviation between the motion of the two rulers?
This is what you observe.
Even if initially similar, the movement of the two rulers become, after a short time, completely different!
The result is the same when initiating more than two motions under similar conditions. This can best be followed by means of a computer simulation. The velocity of the endpoints of 11 rulers started in the same position with slightly different initial speeds looks like this
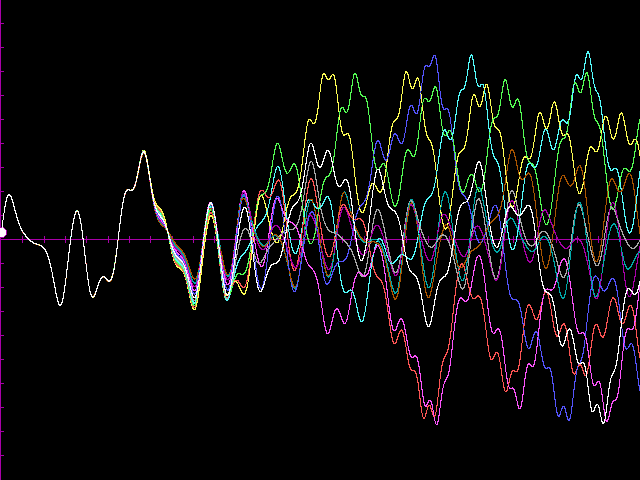
After about five cycles of the electric motor, all rulers behave completely differently. This is not like with ordinary motions. We can thus conclude: small initial uncertainties lead to dramatic differences in the future. In other words, such motions are unpredictable since the final state cannot be predicted due to the small uncertaintes in the preparation of the initial state, which are unavoidable both in experiments and numerical simulations. A widely spread popular expression for this property is 'butterfly effect'. It reminds us in an allegoric way on how small initial uncertaintes leading to dramatic consequences can be (like e.g. the flutter of a butterfly).
More on 'butterfly effect' here.
The American meteorologist Edward Lorenz gave a lecture in 1972 with the title: 'Predictability: Does the Flap of a Butterfly's Wings in Brazil set off a Tornado in Texas?'. The term 'butterfly effect' went into general use due to J. Gleick's popular book entitled 'Chaos: Making a New Science', implicitly suggesting that the answer to the question is affirmative. Outside scientific literature this is often interpreted as if modern sciences would claim that everything is related to everything, and we could not therefore be sure of anything. In contrast to this, the analysis of chaotic systems shows that unpredictability is limited, it only holds on the chaotic attractor. As far as motion before reaching the attractor is concerned, we know for sure that it converges to a very small (but extended) set of zero volume: the attractor. Nearby orbits do not deviate before reaching the attractor. It is worth noting that Lorenz referred in his talk to the difficulties of weather forecasting, but did finally not give an answer to the particular question raised in the title.
If you are interested in how motions can be followed by means of a computer in an easy, Excel-based way, click to this interactive elementary introduction here. By the end of the course, you will be able to run your own chaos simulation, and demonstrate the presence of 'butterfly effect'.
In the language of science we speak of a sensitive dependence on initial conditions rather than the 'buttefly effect'.
Based on both features discussed, try again to answer to the question: what is chaos?
Chaos is a long lasting motion of relatively simple systems, which is
- irregular in time, truly aperiodic, and is not the superposition of periodic components
and
- sensitive to initial conditions: small initial differences are strongly magnified, and are, therefore, unpredicable
It is interesting to see that modern meteorological forecasts are also based on ’plume diagrams’ summarizing the results of an ensemble of 30 different simulations starting from nearly identical states of the atmosphere. Predicted surface temperature for Budapest within a given time interval can be seen on the chart below
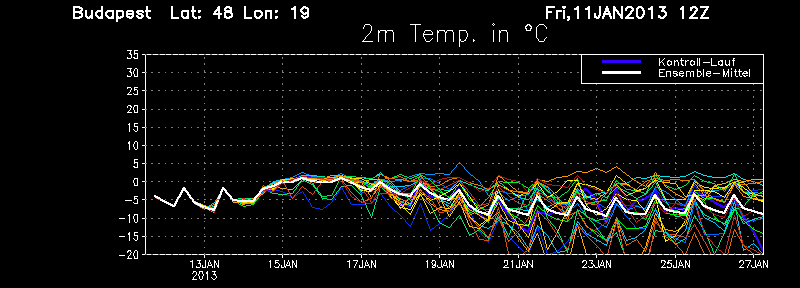
During the first two days, all curves run practically together, but then they start to deviate: a clear demonstration of the 'butterfly effect'. The forecast can thus be considered to be reliable only in the first 3-4 days. For any longer period, weather is unpredictable.
Interested in finding the current ensemble forcast for your city? Visit the public page. On the left, choose your city and the quantity you prefer to follow (e.g. 2m temperature as in our graph, or precipitation) on the bottom. The plum diagram for this quantity of the chosen location appears than for the next two weeks. The white curve represents the mean of all the members followed, the pink one is the obsevred long-time average.
The fact that the 'plume diagrams' are very similar to what we had in our physics experiment, reinforces the view that the motion of a pendulum with a moving suspension point is unpredictable (although the system is much simpler than the atmosphere)!
The length of time interval during which a bunch of initially nearby trajectories stay together is the prediction time $t_p$. For the pendulum experiment $t_p$ is about 6 s, while for the atmosphere $t_p$ is 3-4 days. (The growth rate of initial uncertainties, the so-called Lyapunov exponent, characterizes the strength of chaos, and it can be estimated as the reciprocal of the prediction time for a fixed initial uncertainty. If you want to learn more about the meaning of the prediction time and its typical order of magnitude, consider the problem:
Imagine a chaotic system in which the initial uncertainty, or relative error, $\Delta r_0$ doubles every time unit. After $n$ time units it is $\Delta r(n)=\Delta r_0 2^n$, the growth is exponential. Compare this with a regular system in which the uncertainty grows only linearly, say as $\Delta r(n)=\Delta r_0 (1+2 n)$. Determine the prediction time $t_p$ as the time at which the error is unity: $\Delta r(t_p )=1$. Evaluate $t_p$ in both cases for $\Delta r_0=10^{-6}$ first, and for a much smaller initial uncertainty: $\Delta r_0=10^{-9}$ next.
Answer: In the chaotic case $\Delta r(t_p)=\Delta r_0 2^{t_p}=1$, from which $t_p=\log_2(1/\Delta r_0)$. In the nonchaotic case $t_p=(1/\Delta r_0 -1)/2$. With initial uncertainty $\Delta r_0=10^{-6}$, one finds the prediction time to be $t_p$ approx 20 time units in the chaotic case (since 210 is approximately 1000), while in the regular case $t_p$ approx 5 105. An overwhelming difference! The latter indicates that regular motions can be predicted for any time occuring in practice. The situation becomes more shocking with $\Delta r_0=10^{-9}$. The prediction time grows up to only $t_p=30$ time units for chaos, but becomes 1000 time larger, $t_p=5\ 10^8$ for usual motions. We thus have to conclude: the prediction time of chaotic systems is impossible to increase in practice!