2. Tulajdonság: előrejelezhetetlenség
A káosz újabb jellegzetes tulajdonsága akkor nyilvánul meg, ha összehasonlítunk közel azonos feltételekkel induló mozgásokat. Az előző modul első kísérletében az úgy tehető meg, ha két vonalzót rögzítünk a mozgó tengelyhez úgy, hogy azok párhuzamos síkokban mozoghassanak anélkül, hogy ütköznének. A vonalzók gyakorlatilag azonosak, ugyanattól a gyártótól származnak.
Vársz bármilyen lényegi eltérést a két vonalzó mozgása között?
Itt derül ki, mi történik:
Annak ellenére, hogy a két vonalzó mozgása eleinte azonos, rövid idő után teljesen különbözővé válnak!
Ugyanez történik akkor is, ha kettőnél több mozgást indítunk hasonló feltételekkel. Ezt legjobban számítógépes szimulációkkal követhetjük. Ugyanabból a helyzetből alig különbözö kezdősebességekkel indított 11 azonos vonalzó végponti sebessége látható itt az idő függvényében
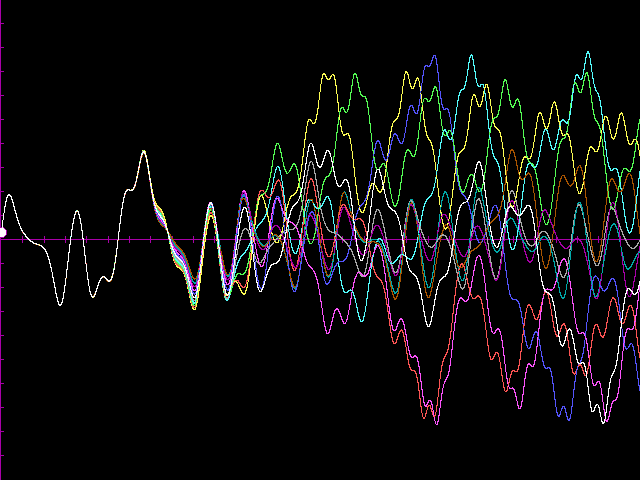
A motor körülbelül öt periódusa után már mindegyik vonalzó teljesen másképpen mozog. Nem ez történne szokásos mozgásokban. Azt mondhatjuk tehát, hogy káoszban a kezdeti bizonytalanságok jelentős jövőbeli különbségekre vezetnek. Más szavakkal, az ilyen mozgás előrejelezhetetlen. A végső állapot nem jósolható meg pontosan a kezdetei állapot meghatározásában jelen levő kis bizonytalanságok miatt, melyek mind kísérletekben, mind szimulálásokban elkerülhetetlenek. Ennek a tulajdonságnak gyakran használt népszerű megfogalmazása a "pillangóeffektus". Ez szimbolikusan arra utal, hogy mennyire csekély lehet az a kezdeti bizonytalanság (akár egy pillangó szárnycsapása), amely drámai következményekkel jár.
A "pillangóeffektusról" többet olvashatsz itt.
Edward Lorenz amerikai meteorológus a következő címmel tartott előadást 1972-ben: "Előrejelezhetetlenség: Okozhat egy brazíliai pilangó szárnycsapása tornádót Texasban?". A "pillangóeffektus" kifejezés J. Gleick könyve, a "Káosz: Egy új tudomány születése" alapján terjedt el, azt sugallva, hogy a feltett kérdésre a válasz igenlő. A szakirodalmon kívül a "pillangóeffektust" gyakran azt sugallmazva használják, hogy a modern tudomány szerint minden mindennel összefügg, s ezért semmiben sem lehetünk biztosak. Ezzel szemben a kaotikus rendszerek vizsgálata azt mutatja, hogy az előrejelezhetetlenség nem terjed ki mindenre, csakis a kaotikus attraktoron (lásd 3. modul) érvényes. Az attraktor elérése előtt a mozgásról biztosan tudjuk, hogy egy nagyon kicsi (de kiterjedt), nulla térfogatú objektumhoz, vagyis az attraktorhoz tart. Közeli mozgások egyáltalán nem válnak szét az attraktor elérése előtt. Érdemes megemlíteni, hogy Lorenz előadásában az időjárás előrejelzésének nehézségére utalt, és nem adott választ a címben feltett konkrét kérdésre.
Ha érdekel, hogyan követhetők mozgások számítógépen, egyszerűen, csak excelre alapozva, kattints az itteni interaktív elemi bevezető anyagra. Ennek áttanulmányozása után képes leszel arra, hogy saját káosz-szimulációdat futtasd, és átéld a "pillangóeffektust".
A tudományos nyelvezet a "pillangóeffektus" helyett a "kezdőfeltételektől való érzékenység" kifejezést használja.
Az eddig vizsgált két tulajdonság alapján, mit válaszolnál arra a kérdésre, hogy mi a káosz? Teljesebb válasz
A káosz egyszerű rendszerek olyan hosszú idejű viselkedése, amely
- időben szabálytalan, teljesen aperiodikus,
és
- érzékeny a kezdőfeltételekre: kis kezdeti különbségek, erősen felnagyítódnak, ezért a mozgás előrejelezhetetlen
Érdemes tudni, hogy a modern időjárási előrejelzések ún "fáklyadiagramokat" is közreadnak, melyek a légkör állapotának 30 különböző futtatási eredményét foglalják össze, közel azonos kiindulási állapotokból indulva. A következő ábrán a Budapestre vonatkozó felszíni hőmérséklet előrejelzése látható adott időintervallumra
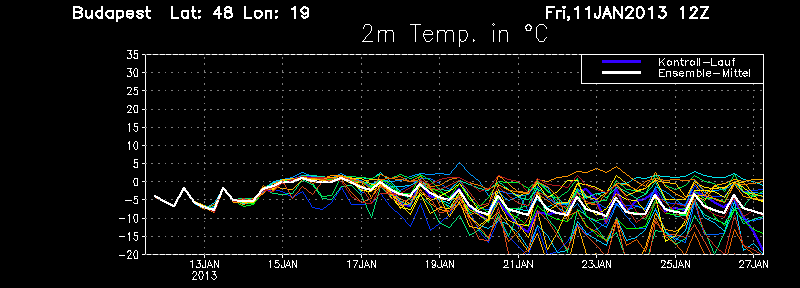
Az első néhány nap alatt minden görbe gyakorlatilag együtt halad, de azután erősen eltérnek: ez a "pillangóeffektus" közvetlen megnyilvánulása. Az előrejelzés ezért csak az első 3-4 napra tekinthető megbízhatónak. Hosszabb távra az időjárás előrejelezhetetlen.
Érdekel, hol érhető el a lakóhelyedre vonatkozó aktuális élőrejelzés? Látogass el erre a nyilvános lapra. A bal oldalon kiválaszthatod városod, lent a követni kivánt légköri mennyiséget (pl. a 2 méteren mérhető hőmérsékletet vagy a csapadékot). A megjelenő fáklyadiagram a kattintás utáni két hétre vonatkozik. Rajta a fehér görbe az összes futtatás átlagát jelenti, a lila a korábbi megfigyelések sokéves átlagát.
Az a megfigyelés, hogy a fáklyadiagramok hasonlítanak a fizikai kísérletünkben kapotthoz, megerősíti, hogy a mozgó felfüggesztési pontú inga mozgása előrejelezhetetlen (noha a rendszer sokkal egyszerűbb, mint a légkör)!
Annak az időszaknak a hossza, melynek során a kezdetben közeli mozgások közel maradnak egymáshoz, a $t_e$ előrejelzési idő. Az ingakísérletben $t_e$ korülbelül 6 másodperc, a légkör esetében pedig 3-4 nap. (A kezdeti bizonytalanságok időbeli növekedési üteme, az ún. Ljapunov-exponens, a chaos erősségét méri. Ez a mennyiség megbecsülhető az előrejelzési idő reciprokaként, ha a kezdeti bizonytalanság rögzített.) Ha többet szeretnél tudni az előrejelzési idő jelentéséről és tipikus értékeiről, nézz bele a következő feladatba:
Tekintsunk egy kaotikus rendszert, melyben a kezdeti bizonytalanság, vagy relatív hiba, $\Delta r_0$, időegységenként megkétszereződik. $n$ időegység után tehát a bizonytalanság, hiba $\Delta r(n)=\Delta r_0 2^n$, vagyis exponenciálisan nő. Hasonlítsuk ezt össze a szabályos rendszerek esetével, amikoris a bizonytalanság, hiba csak (legfeljebb) lineárisan nő, vagyis például $\Delta r(n)=\Delta r_0 (1+2 n)$. A $t_e$ előrejelzési idő az az idő, amikorra a hiba nagyon naggyá, mondjuk egységnyivé válik: $\Delta r(t_e )=1$. Határozzuk, meg $t_e$-t mindkét esetben, ha kezdetben $\Delta r_0=10^{-6}$, és akkor is, ha a kezdeti bzonytalanság sokkal kisebb, $\Delta r_0=10^{-9}$. Megoldás
Megoldás: A kaotikus esetben $\Delta r(t_e)=\Delta r_0 2^{t_e}=1$, amiből $t_e=\log_2(1/\Delta r_0)$. Szabályos mozgás esetén $t_e=(1/\Delta r_0 -1)/2$. Kezdeti $\Delta r_0=10^{-6}$ bizonytalansággal azt kapjuk, hogy $t_e$ körülbelül 20 idóegység a kaotikus esetben (mivel 210 becsülhető 1000-el), míg a szabályos esetben $t_e$ körülbelül 5 105. Hatalmas különbség! A második eredmény mutatja, hogy a szabályos mozgások gyakorlatilag bármeddig előrejelezhetőek. Az eredmény még megrázóbbá válik a lényegesen csökkentett $\Delta r_0=10^{-9}$ kezdeti hibával. Az előrejelzési idő káoszban alig nő valamit, $t_e$ 30-ra változik, de szokásos mozgásokra 1000-szeresére nő: $t_e=5\ 10^8$ egység. Meg kell, hogy fogalmazzuk: az előrejelzési idő csökkentése kaotikus rendszerekben gyakorlatilag lehetetlen.