I. The basic effect: deflection of moving bodies
Carry out a simple home experiment with a pencil, a paper disk, and a ruler. Fix the center of the paper disk to a board with a pin. First draw a straight line from the center at a constant speed on the non-moving sheet. Repeat the same motion with someone rotating the sheet clockwise at an approximately constant angular velocity, see video4, while you are drawing the line. You will obtain a curved path, deflecting from the straight line, similar to this.
It is clear that the motion on the carousel (like the path traced out on the rotated paper sheet) is deflected from its initial direction. Note that the deflection is to the left if the rotation is clockwise. The same kind of deflection is observed in the deflection of the ball and of the line drawn in video2 and video4, respectively.
Note: the straight line on the non-rotated paper sheet corresponds to a uniform motion as seen from stationary reference frame. The deflection is thus a consequence of the fact that an otherwise simple motion is observed from a rotating frame.
The curved path traced out on the rotated paper sheet resembles a parabola, at least for short distances. The motion relative to the carousel is thus similar to motion with a constant acceleration.
In the curve drawn in your experiment, consider the part that belongs to short times (i.e. the part near the beginning). Measure the amount of deflection from the straight line at a few points.
1. Using the displacement along the straight line as a measure of time (in arbitrary units), show that the dependence is parabolic for short times at least, and determine the acceleration.
2. Using the fact that a point of distance $r$ from the center is rotated along an arc of length $r \Omega t$, where $\Omega$ is the angular velocity of the sheet, express the acceleration in terms of $\Omega$ and the pencil’s velocity $v$. Find the force that causes this acceleration.
The force used to describe the deviation is the Coriolis force. Its magnitude is $$ {F_C=m 2 v \Omega}, $$ and it points perpendicular to the direction of velocity $\boldsymbol{v}$, to the left and to the right in the case of clockwise and counter-clockwise rotation, respectively.
3.
For a deeper insight, carry
out a slightly more advanced experiment. Repeat the first experiment so that you start drawing the pencil line at a
distance of $r_0$ away from the center of rotation and radially outwards, video5.
Will you obtain a different expression for the acceleration or the force acting perpendicular to the velocity?
The force remains $F_C=m 2 v \Omega$ but $v$ turns out to be the velocity of the body relative to the rotating system. Another force also appears acting radially outwards, this is the centrifugal force $F_{cf}=m r_0 \Omega^2$. Both forces are important in the motion of a ball on the carousel, but only the Coriolis force is responsible for the deflection from the original velocity.
A basic quantitative measure: the strength of deflection
Consider a body which would move in a non-rotating system with a velocity of $U$ and estimate the deflection $D$ due to the Coriolis force from the direction of this initial velocity after traveling a distance $L$.
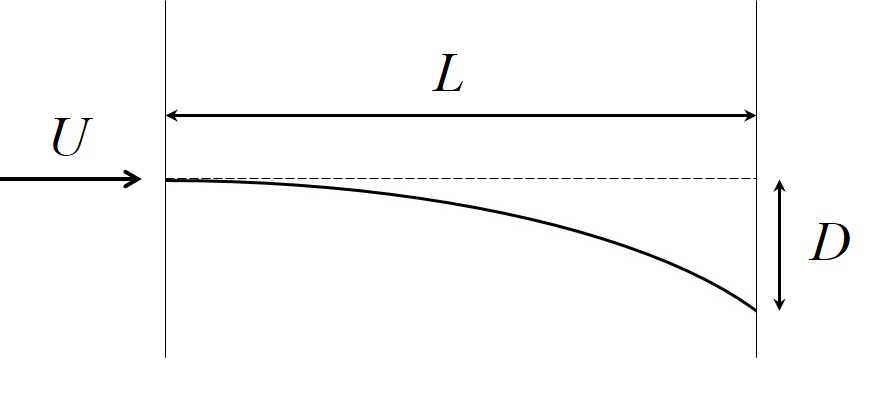
Assume that the deflection is very small compared to the distance $L$ ($D \ll L)$. The acceleration $2 v \Omega$ is then constant and can be approximated by $2 U \Omega$. With this approximation, the distance $D$ traveled perpendicular to the initial velocity is, after time $t$, $(1/2)a_C t^2$, i.e., $(1/2) 2 U \Omega t^2$. The time needed to travel a distance $L$ is approximately $L/U$, and we obtain $$D=U \Omega L^2 /U^2 = \Omega L^2 /U.$$ The relative deflection, the distance $D$ compared to the total distance $L$, i.e. $D/L$ is also worth considering: $$ \boxed{D/L = \Omega L/U.} $$ This is a useful simple expression which can serve to estimate the magnitude of the Coriolis deflection. In more general cases, $U$ should be taken as the average speed of the motion. The expression $D/L=\Omega L/U$ for the relative deflection is generally considered the quantitative measure of the strength of deflection. Note that it is inversely proportional to $U$ since not only the acceleration counts, the time during which the Coriolis force acts is also important for the deflection.
