II. The rotating Earth as a carousel
The paper sheet experiment clearly illustrates that deflection is due to a rotation, the axis of which is perpendicular to the plane in which the deflection takes place. If the plane of deflection is not perpendicular to the rotational axis, it is the angular velocity component perpendicular to this plane that determines the rate of deflection.
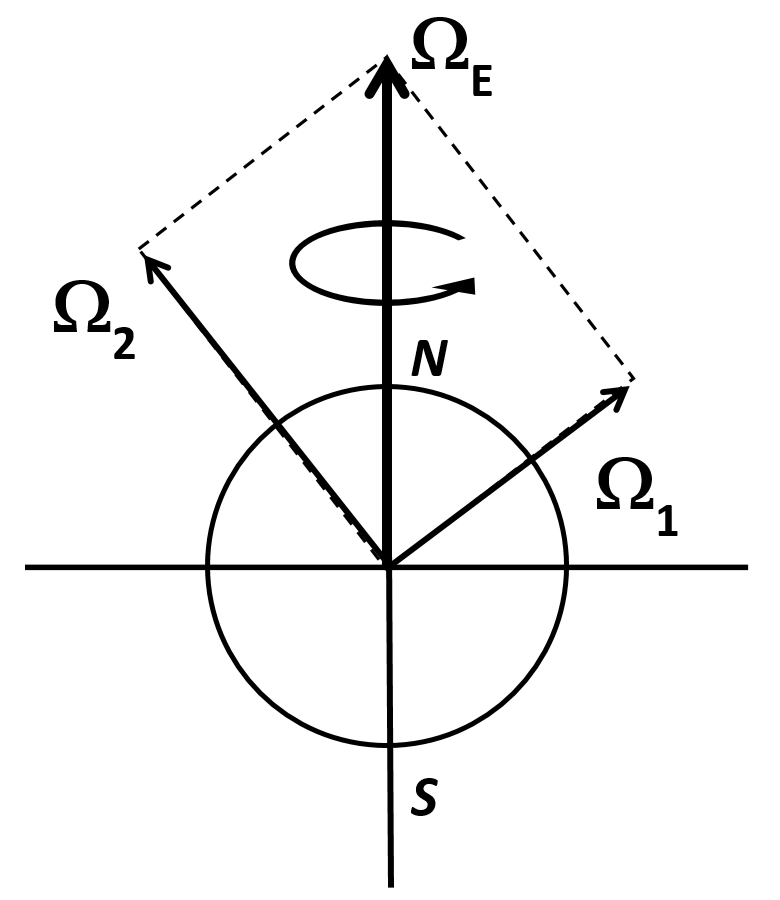
It must be surprising to learn that angular velocity may have components. In fact, it is useful to consider angular velocity a vector. The angular velocity vector is parallel to the axis of rotation, and its direction is obtained as the direction of the thumb of one’s right hand if the fingers are curved in the direction of the rotation. Besides directionality, angular velocity is a vector also in the sense that it can be decomposed into perpendicular components. This implies that a rotation through a small angle, with an angular velocity vector ${\bf \Omega}$ is equivalent to carrying out rotation around one axis with angular velocity ${\bf \Omega_1}$ and, another rotation around a perpendicular axis with angular velocity ${\bf \Omega_2}$, where $\Omega^2=\Omega_1^2+\Omega_2^2$. This is illustrated by means of a simple animation. (Note that the animation is not to scale since the decomposition of angular displacement into two components about two perpendicular axes holds true for small angles only which would not be visible otherwise.)
When applied to the rotating Earth, the angular velocity ${\bf \Omega_E}$ of the planet directed along the axis from south to north can be decomposed into arbitrary perpendicular components ${\bf \Omega_1}$ and ${\bf \Omega_2}$, as shown here
For describing the deflection effect of the Coriolis force on the Earth — which is always observed in the local horizontal plane — it is most natural to decompose ${\bf \Omega_E}$ into horizontal and vertical components at a geographical location with magnitudes denoted by $\Omega_H$ and $\Omega_V$, respectively.
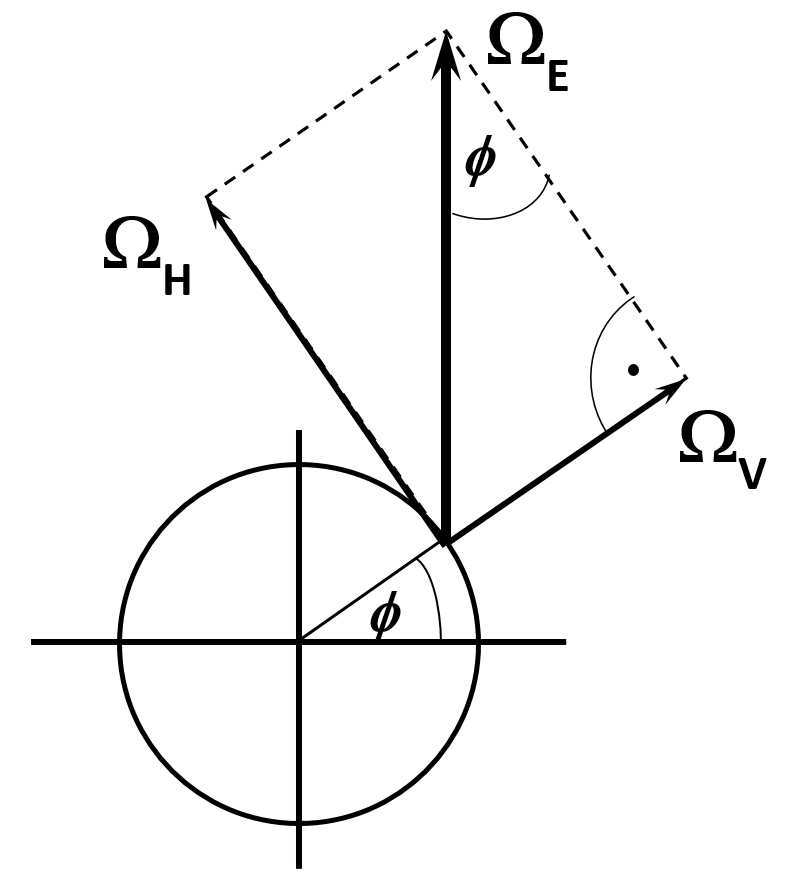
If you are interested to see that the resultant angular velocity is indeed the vector sum of the horizontal and vertical components in this particular decomposition, too, consult this page.
At a geographical latitude $\phi$, the angle between the horizontal plane and the rotation axis is also $\phi$ (see the figure above), therefore the angular velocity component of Earth, $\Omega_E$, projected onto the local vertical is $$ {\Omega_V = \Omega_E \sin \phi} . $$
The deflection expression $D=\Omega L^2 /U$ can safely be applied to any motion on the Earth, you just have to replace $\Omega$ with $\Omega_V$. The relative deflection can then be given as $$ \boxed{D/L = \Omega_V L/U.} $$ Note that the Earth's angular velocity is 1 rotation / 1 day = $2 \pi/ 86400 \text{ s}$, i.e., $$ \Omega_E=7.3 \cdot 10^{-5} \text{ 1/s}. $$ At mid latitudes, at $\phi \sim 45 \text{ degrees} (=\pi/4)$, $$ \Omega_V=5 \cdot 10^{-5} \text{ 1/s}, $$ a value easy to remember. Note that on the Southern Hemisphere $\phi$ is negative, and thus $\Omega_V$ is negative, too.
Remark: A simplifying feature in motions on the Earth as compared to those on a carousel is that the centrifugal force need not be taken into account explicitly, since it is included in the acceleration of gravity: the acceleration of gravity ${\bf g}$ is the vector sum resulting from the gravitational and the (small) centrifugal acceleration.
4. Application: Estimate the deflection of a cannon ball shot from the gun in the picture, to a distance of L=100 km
at mid latitudes During World War I, given that the average horizontal velocity of the canon ball from the gun was about 500 m/s.
$$ \Omega_V = 5 \cdot 10^{-5} \text{ 1/s},\ L=10^5 \text{ m},\ U=500 \text{ m/s},\quad \text{thus} \quad D=\Omega_V L^2/U = 1 \text{ km}. $$ Coriolis compensators letting the canon shoot a little left of the target on the Northern Hemisphere (by approximately 1/100 radians, about 0.6 degrees in this case) were used during World War I.
Does water drain in different directions on the Northern and Southern Hemispheres?
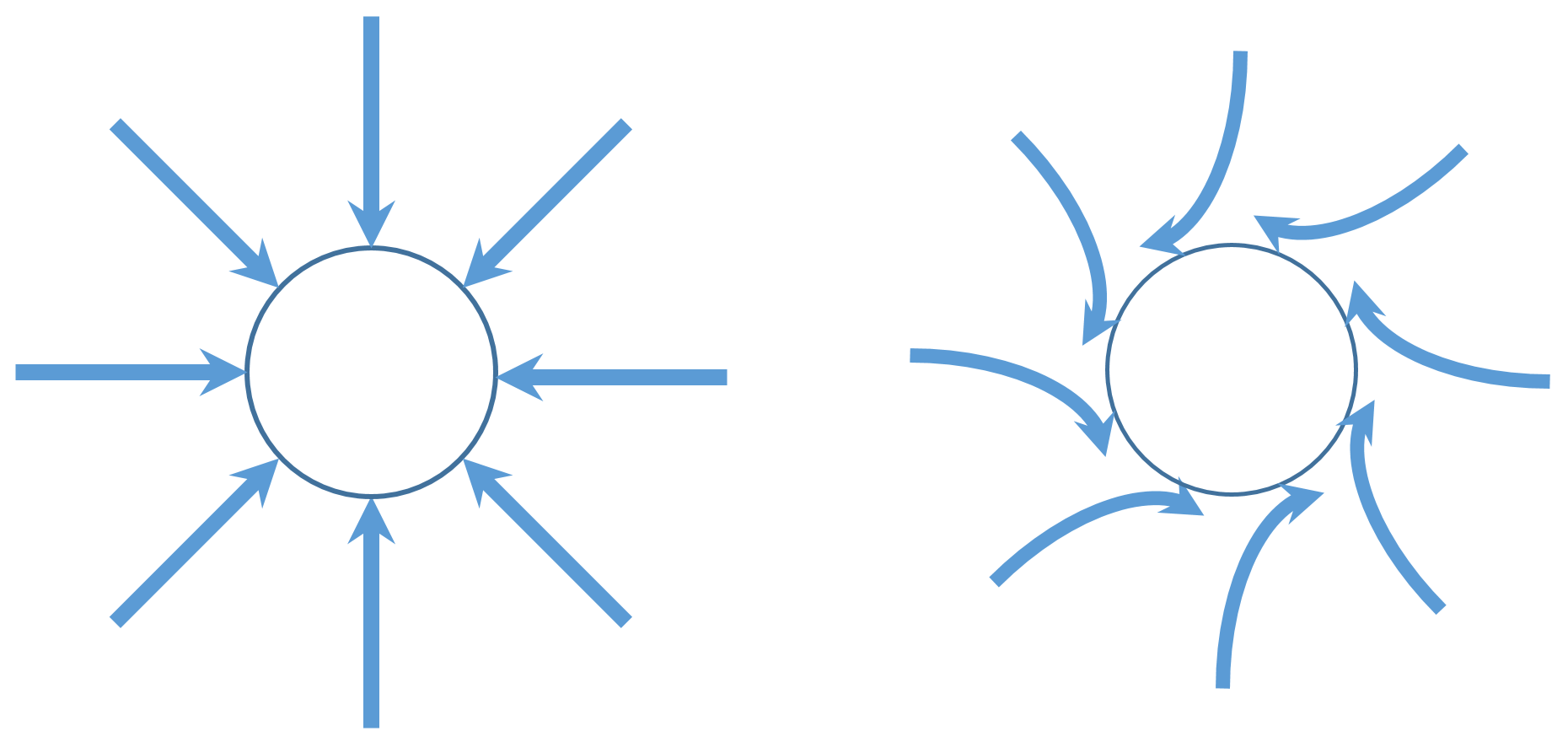
If the Coriolis force were acting alone, it would be reasonable to think that water drains differently on the two hemispheres, since the sign of $\Omega_V$ is different, as seen above. When draining starts, water parcels start to move towards the sink, but become deflected due to the Coriolis force. The figure below corresponds to the Northern Hemisphere where a counter-clockwise spin is expected while water is going down a plughole.
5. Before becoming fully convinced, estimate the deflection $D$ at mid latitudes, using realistic values for a plughole: $L=10 \text{ cm},\ U=10 \text{ cm/s}$.
$$ \Omega_V = 5 \cdot 10^{-5} \text{ 1/s},\ L=0.1 \text{ m},\ U=0.1 \text{ m/s},\quad \text{thus}\quad D=\Omega_V L^2 /U = 5 \cdot 10^{-6} \text{ m} \;\;\; (D/L= 5 \cdot 10^{-5} ).$$ This value equals 5 micrometers, which cannot be perceived by the eye! The fact that this number is so small is the reason why our laboratories can be considered inertial reference frames in which Newton’s law hold, since the Coriolis force is practically negligble.
6.
To see how strong other effects
can be in the draining process, consider a small cuboid of water bounded by two vertical faces of area $A$ separated by
a horizontal distance of $\Delta r=1 \text{ cm}$. Estimate the acceleration caused by the difference in the hydrostatic
pressure generated by a tiny height difference: $\Delta h=0.1\text{ mm}$ on the surfaces of the opposite vertical faces
of the cuboid.
The Coriolis deflection is so small, due to the small magnitude of Earth’s angular velocity, that this effect is typically suppressed in our bath tubs by other effects (residual fluid motion, waves on the surface, asymmetry of the container, etc.) and in practice, either direction of the plughole vortex may be observed on either hemisphere. In carefully planned experiments, however, where all the disturbances are ruled out, the expected direction of spin can indeed be observed. The first such experiment was carried out by A. Perrot in Paris in 1859.
Read about more recent experiments with sinks.
7. Considering all these, how can you explain the events seen in the very first video? Hint: On the Equator (where the local horizontal plane is parallel to the rotational axis), what is the magnitude of $\Omega_V$, which is responsible for the deflection?
Since the total angular velocity vector points to the North, it has no vertical component here: $\Omega_V=0$. Therefore, no deflection occurs at the Equator! The effect seen in the video must be due to a clever way of pouring the water into the vessel.
Examples with evidence for (a weak) Coriolis deflection
The deflection effect is so weak that it cannot be detected in household plugholes, while in other cases its presence can be demonstrated by means of specially tailored experiments, or very careful or long-lasting observations. Two such experiments play an important role in the history of physics since they provided evidence for the rotation of the Earth:
Read about the experiment by Foucault.
8. What is the Foucault period $T_F$ a) at the North Pole, and b) at the Equator?
a) 1 day, b) the pendulum does not rotate at the Equator.
Read about the experiment by Eötvös.
9. How much lighter will a person of mass $m=100\text{ kg}$ get when sitting in a car moving to the East with $30\text{ m/s}$ at mid latitudes?
The magnitude of the Eötvös force for a typical velocity $U$ is $F_E=2 m \; \Omega \; U =2 \cdot 100 \cdot 0.5 \cdot 10^{-4} \cdot 30 \;\;\text{ N} = 0.3 \;\text{ N}$ corresponding to the weight of a mass of $30$ g.
10. At which latitude on Earth is the Eötvös effect the most pronounced?
At the Equator.
Read about other weak deflection effects which, occasionally, may have long-lasting consequences.
On the Northern Hemisphere, the right bank of rivers is eroding faster than the left one. This rule was formulated (in a somewhat restricted form) by the Estonian scientist K. E. Baer in 1860.
On geological time scales, the Coriolis force might cause river beds to drift hundreds of kilometers to the right of the overall direction of the river.
On the Northern Hemisphere, the wear on the right rail of railway tracks is stronger than that on the left rail.
In sports like hammer or javelin throw, deflection due to the Coriolis force can be on the order of a few cm.
11.Given that an aircraft is
moving at a speed of $1080$ km/h, estimate the tilt angle needed to compensate for the Coriolis deflection.
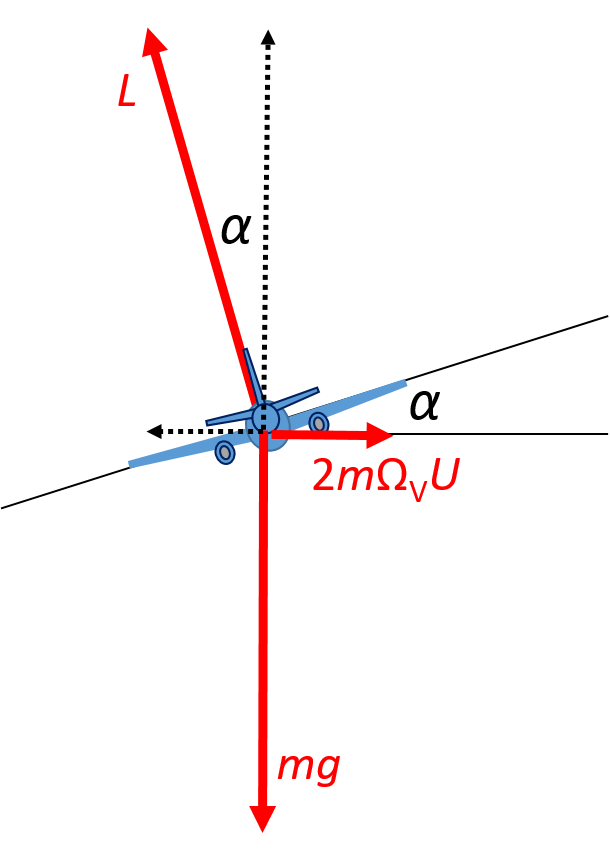
On the Northern Hemisphere the aircraft should tilt to the left at
some angle $\alpha$ (as if it intended to turn left) to compensate for the Coriolis force pointing
to the right of its direction of flight.
The lift force $L$ acting perpendicular to the wings compensates for the weight $mg$
of the craft $L \cos\alpha= mg$.
%under this weak tilt, too. Since the aircraft is tilted,
The horizontal component of this force is
$L \sin\alpha=mg \tan\alpha$. This should balance the deflecting force to the right:
$$ mg \tan\alpha = 2 m \Omega_V U. $$
Under this weak tilt $\tan\alpha \approx \alpha$, and thus $\alpha = 2 \Omega_V U/g$. When $U=300 \text{ m/s}$,
$\alpha=3 \cdot 10^{-3} \text{ rad} = 0,17 \text{ degrees}$, very small.
On the human scale, from a few meters up to hundreds of meters, the Coriolis effect is weak: in certain situations it cannot even be perceived, while in others one has to use special equipment to prove it in experiments.
12. How about larger scales? Evaluate the ratio $\Omega_V L/U$ at mid latitude for a typical horizontal speed of $U=10$ m/s on increasing length scales of the size of $L=10, 100, 1000$ and $10000$ km. Express the ratio as a percentage. What is your conclusion regarding the importance of the deflection on these scales?
| $L$ | $\Omega_V L/U$ | ($\Omega_V=5 \cdot 10^{-5} \text{ 1/s},\quad U=10 \text{ m/s}$) |
|---|---|---|
| 1 km | 0.5% | deflection effect is very weak |
| 10 km | 5% | deflection effect becomes noticable |
| 100 km | 50% | deflection effect is considerable |
| 1000 km | 500% | deflection effect dominates |
Observe that Coriolis deflection becomes more relevant with increasing scales.
