II. A forgó Föld mint körhinta
A papírkorongos kísérletből jól látható, hogy az eltérülést az eltérülés síkjára merőleges tengely körüli forgás okozza. Amikor az eltérülés síkja nem merőleges a forgástengelyre, akkor azonban a szögsebességnek erre a síkra merőleges komponense határozza meg az eltérítés mértékét.
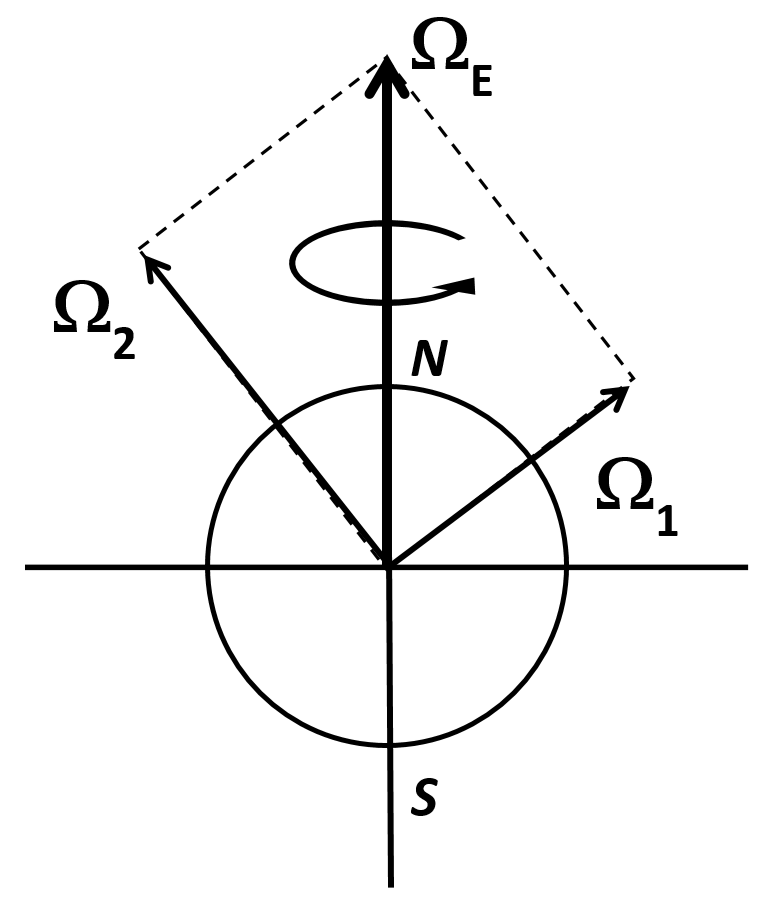
Bizonyára meglepően hangzik, hogy a szögsebességnek komponensei vannak, ám a szögsebességet valóban érdemes vektornak tekinteni. A szögsebességvektor állása párhuzamos a forgástengellyel, irányát pedig a jobb kezünk hüvelykujjának iránya adja meg, hogyha a meggörbített többi ujjunk a forgás irányába mutat. A vektortermészet nemcsak az irányítottságban mutatkozik meg: a szögsebességvektort fel is lehet bontani merőleges komponensekre. Ebből az következik, hogy egy igen kicsi szöggel történő ${\bf \Omega}$ szögsebességű elfordulás ekvivalens egy valamely tengely körüli ${\bf \Omega_1}$ szögsebességű elfordulás, valamint egy rá merőleges tengely körüli ${\bf \Omega_2}$ szögsebességű elfordulás kompozíciójával, ahol $\Omega^2=\Omega_1^2+\Omega_2^2$. Ezt szemlélteti az itt látható egyszerű animáció. (Az animáció nem méretarányos, hiszen a szögelfordulásra csak nagyon kicsi szögek esetén alkalmazható a merőleges komponensekre való felbontás, ezért a láthatóság végett itt a szögelfordulások eltúlzott mértékűek.)
A forgó Föld esetében ily módon a bolygó ${\bf \Omega_F}$ szögsebességvektora tengelyirányú, és déltől észak felé mutat. Ahogyan itt látható, ezt is tetszőlegesen felbonthatjuk az ${\bf \Omega_1}$ és ${\bf \Omega_2}$ merőleges komponensekre.
Amikor a Coriolis-erő hatására fellépő eltérülést akarjuk leírni — amelyet a forgó Földön mindig a helyi vízszintes síkban tudunk megfigyelni — természetes módon kínálkozik, hogy az ${\bf \Omega_F}$ szögsebességet az adott földrajzi helynek megfelelő vízszintes (azaz horizontális) és függőleges (vertikális) komponensekre bontsuk fel, melyek nagyságát itt $\Omega_H$, illetve $\Omega_V$ jelöli.
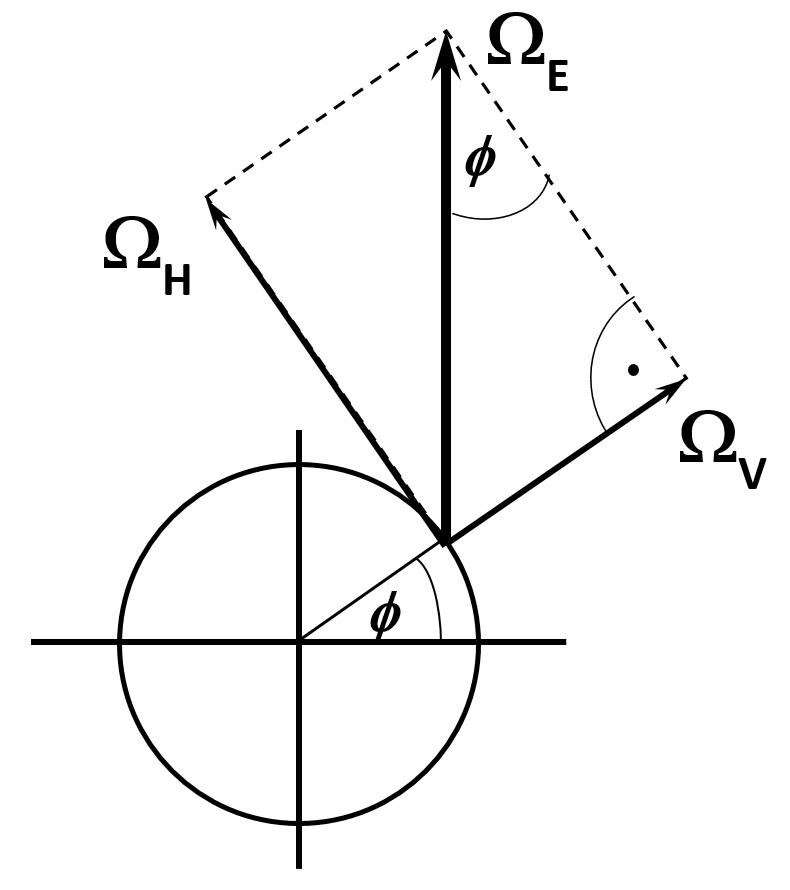
Ha szeretnél más módon is meggyőződni arról, hogy az eredő szögsebesség valóban a vízszintes és függőleges komponensek vektori összege, itt tájékozódhatsz.
Ahol a földrajzi szélessg $\phi$, ott a vízszintes sík és a forgástengely szöge ugyancsak $\phi$ (lásd a fenti ábrát), tehát a Föld $\Omega_F$ szögsebességvektorának a helyi függőlegesre való vetülete $$ {\Omega_V = \Omega_F \sin \phi}. $$
Az eltérülésre kapott $D=\Omega L^2 /U$ kifejezést nyugodtan alkalmazhatjuk a Földön zajló bármilyen mozgásra, csak éppen az $\Omega$ szögsebesség helyére kell $\Omega_V$ szögsebességet írnunk. A relatív eltérülésre így $$ \boxed{D/L = \Omega_V L/U} $$ adódik. Tudjuk, hogy a Föld szögsebessége 1 fordulat / 1 nap = $2 \pi/ 86400 \text{ s}$, vagyis $$ \Omega_F=7.3 \cdot 10^{-5} \text{ 1/s}. $$ Közepes szélességeken, ahol $\phi \sim 45 \text{ fok} (=\pi/4)$, $$ \Omega_V=5 \cdot 10^{-5} \text{ 1/s}. $$ Ezt az értéket könnyű megjegyezni. Ne felejtsük el, hogy a Déli-féltekén $\phi$ negatív, és így $\Omega_V$ szintén negatív.
Megjegyzés: A körhintával összehasonlítva a Földön zajló mozgások tárgyalását leegyszerűsíti, hogy a centrifugális erővel külön, explicit módon nem kell foglalkoznunk, mivel benne van a nehézségi gyorsulásban: a ${\bf g}$ nehézségi gyorsulás a gravitációs gyorsulásnak és az igen kicsi centrifugális gyorsulásnak az eredője.
 4. Alkalmazás: A képen látható ágyút az Első Világháborúban használták. A lövedék átlagos vízszintes sebessége
körülbelül 500 m/s volt. Adj becslést a közepes földrajzi szélességen L=100 km távolságba lőtt lövedék eltérülésére.
4. Alkalmazás: A képen látható ágyút az Első Világháborúban használták. A lövedék átlagos vízszintes sebessége
körülbelül 500 m/s volt. Adj becslést a közepes földrajzi szélességen L=100 km távolságba lőtt lövedék eltérülésére.
$$ \Omega_V = 5 \cdot 10^{-5} \text{ 1/s},\ L=10^5 \text{ m},\ U=500 \text{ m/s},\quad \text{ ahonnan} \quad D=\Omega_V L^2/U = 1 \text{ km}. $$ Az Első Világháborúban Coriolis-kompenzátort is alkalmaztak, amely az Északi-féltekén kissé a célponttól balra irányította a lövedéket (ebben az esetben körülbelül 1/100 radiánnal, azaz 0,6 fokkal).
Igaz, hogy a lefolyók ellentétes irányban örvénylenek az Északi, illetve a Déli-féltekén?

Ha egyedül a Coriolis-erő hatna, logikus következtetés lenne, hogy a víz ellenkező irányban örvénylik a két féltekén, hiszen láttuk, hogy $\Omega_V$ különböző előjelű. Amikor a víz elkezd lefolyni, a vízrészecskék a lefolyó irányába indulnak, de a Coriolis-erő eltéríti őket. Az ábra az Északi-féltekére vonatkozik, ahol ez alapján azt várnánk, hogy a lefolyóba távozó víz az óra járásával ellentétesen örvénylik.

5. Mielőtt azonban elhamarkodottan ítélnél, becsüld meg a $D$ eltérülés nagyságát közepes földrajzi szélességen: legyenek a lefolyóra jellemző reális értékek $L=10 \text{ cm},\ U=10 \text{ cm/s}$.
$$ \Omega_V = 5 \cdot 10^{-5} \text{ 1/s},\ L=0.1 \text{ m},\ U=0.1 \text{ m/s},\quad \text{így}\quad D=\Omega_V L^2 /U = 5 \cdot 10^{-6} \text{ m} \;\;\; (D/L= 5 \cdot 10^{-5} ).$$ Ez 5 mikrométernyi eltérülést jelent, ami szemmel észrevehetetlen! Éppen ennek az értéknek a kicsinysége teszi lehetővé, hogy a laboratóriumot inerciarendszernek tekinthessük, ahol teljesülnek Newton törvényei, mivel a Coriolis-erő gyakorlatilag elhanyagolható.
6. A lefolyóba távozó víz mozgását befolyásoló
más hatások erősségének vizsgálatához tekintsünk egy vízzel kitöltött kisméretű téglatestet: két függőleges lapjának területe
legyen $A$, vízszintes távolságuk pedig $\Delta r=1 \text{ cm}$. Becsüld meg, hogy $\Delta h=0.1\text{ mm}$ magasságkülönbség
esetén mekkora vízszintes gyorsulást okoz a téglatest két szemközti lapjára ható hidrosztatikai nyomások eltérése.
A lefolyóba távozó víz mozgását befolyásoló
más hatások erősségének vizsgálatához tekintsünk egy vízzel kitöltött kisméretű téglatestet: két függőleges lapjának területe
legyen $A$, vízszintes távolságuk pedig $\Delta r=1 \text{ cm}$. Becsüld meg, hogy $\Delta h=0.1\text{ mm}$ magasságkülönbség
esetén mekkora vízszintes gyorsulást okoz a téglatest két szemközti lapjára ható hidrosztatikai nyomások eltérése.
A Földforgás kis szögsebessége miatt a fürdőkádban a Coriolis-eltérülés annyira kicsi, hogy ezt a hatást általában elfedik más hatások (a folyadék meglévő mozgásai, a vízfelület hullámzása, a tartály aszimmetriája,stb.), ezért a lefolyóban bármelyik irányú örvénylés létrejöhet bármelyik féltekén. A magyar nyelvterületen mintegy 300 háztartási lefolyóban végzett megfigyelés összesített eredménye ebben a blogban olvasható. Gondosan megtervezett kísérleti körülmények között azonban az egyéb zavaró hatások mind kiküszöbölhetők, és valóban megfigyelhető a várt irányú örvénylés. Az első ilyen kísérletet 1859-ben végezte A. Perrot Párizsban.
Itt olvashatsz lefolyókkal végzett későbbi kísérletekről.
7. Mindezek tükrében adj magyarázatot a legelső videóban látottakra. Segíthet, ha meggondolod, hogy mekkora az eltérülésért felelős $\Omega_V$ komponens az Egyenlítőn (ahol a helyi vízszintes sík párhuzamos a forgástengellyel).
Mivel a teljes szögsebességvektor északra mutat, függőleges komponense ezúttal nincs: $\Omega_V=0$. Az Egyenlítőn tehát nem történik eltérülés! A videóban látott örvénylés csak azáltal jöhet létre, hogy a vizet ügyesen megválasztott irányból öntik bele az edénybe.
Példák a (gyenge) Coriolis-hatás megnyilvánulására
Az eltérítő hatás olyan gyenge, hogy az otthoni lefolyókban nem lehet megfigyelni. Kimutatásához gondosan megtervezett kísérletekre vagy nagyon hosszú ideig folytatott alapos megfigyelésre van szükség. Két ilyen kísérlet fontos szerepet játszott a fizika történetében, mert közvetlen bizonyítékul szolgáltak arra, hogy forog a Föld:
Itt olvashatsz Foucault kísérletéről.
8. Mennyi a Foucault-inga $T_F$ körülfordulási ideje a) az Északi-sarkon, illetve b) az Egyenlítőn?
a) 1 nap, b) az Egyenlítőnél az inga nem fordul körbe.
Itt olvashatsz Eötvös kísérletéről.
9. Mennyivel lesz könnyebb egy $m=100\text{ kg}$ tömegű ember, ha közepes fördrajzi szélességen egy $30\text{ m/s}$ sebességgel kelet felé haladó autóban ül?
Ha a tipikus sebesség $U$, az Eötvös-erő nagysága $F_E=2 m \; \Omega \; U =2 \cdot 100 \cdot 0.5 \cdot 10^{-4} \cdot 30 \;\;\text{ N} = 0.3 \;\text{ N}$, ami $30$ g tömegnek megfelelő súlycsökkenést jelent.
10. Az Eötvös-hatás milyen földrajzi szélességen a legjelentősebb?
Az Egyenlítőn.
Itt olvashatsz a gyenge eltérülés további eseteiről, amelyek időnként hoszú távú következményekkel is járhatnak.
Az Északi-féltekén a folyók jobb partja gyorsabban erodálódik, mint a bal part. Ezt a törvényszerűséget (valamivel szűkebb formában) K. E. Baer észt tudós fogalmazta meg 1860-ban.

Geológiai léptékű idő alatt a Coriolis-erő hatására a folyómedrek több száz kilométerrel is eltolódhatnak a jellemző folyásiránytól jobb felé.
Az Északi-féltekén a jobb oldali vasúti sín erősebben kopik, mint a bal.
Egyes sportágakban (kalapácsvetés, gerelyhajítás) a Coriolis-eltérülés mértéke néhány cm is lehet. Erről bővebben olvashatsz Horváth Gábor: Biomechanika c. könyve 8. fejezetében (ELTE Eötvös Kiadó, Budapest, 2009)
11. Egy repülőgép sebessége
$1080$ km/h. Becsüld meg, hogy a Coriolis-eltérülés kompenzálásához mekkora szöggel kell megdönteni a gépet.
Egy repülőgép sebessége
$1080$ km/h. Becsüld meg, hogy a Coriolis-eltérülés kompenzálásához mekkora szöggel kell megdönteni a gépet.
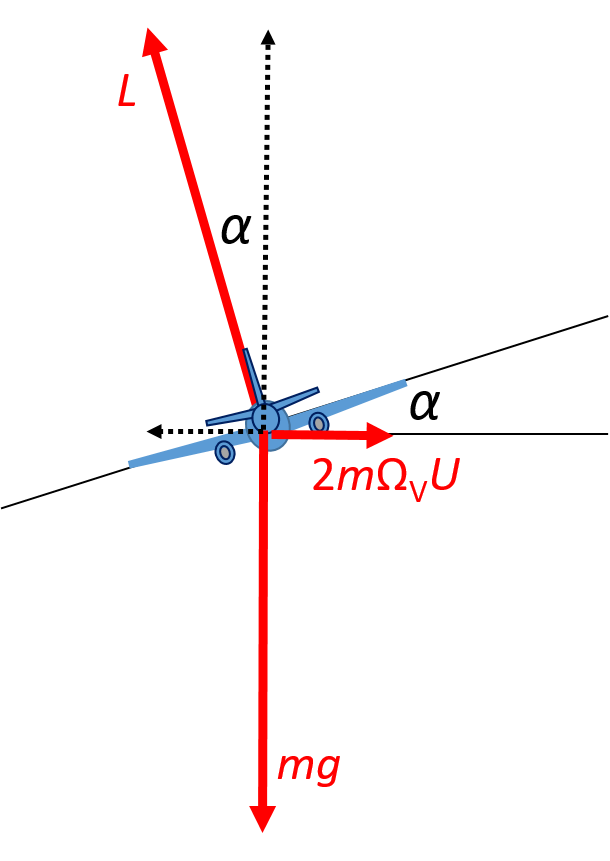
Az Északi-féltekén a haladás irányához képest jobb felé ható Coriolis-erő kompenzálásához a repülőgépet
balra kell dönteni (mintha balra akarna kanyarodni). Keressük az ehhez szükséges $\alpha$ dőlésszöget.
A szárnyak síkjára merőleges $L$ emelőerő függőleges komponense egyenlő az $mg$ nehézségi erővel: $L \cos\alpha= mg$.
Mivel a repülőgép oldalra dől, az emelőerő vízszintes komponense $L \sin\alpha=mg \tan\alpha$. Ennek kell egyensúlyban
lennie a jobb felé ható eltérítő erővel:
$$ mg \tan\alpha = 2 m \Omega_V U. $$
Mivel a dőlésszög kicsi, $\tan\alpha \approx \alpha$, így $\alpha = 2 \Omega_V U/g$. $U=300 \text{ m/s}$ esetén a szög
$\alpha=3 \cdot 10^{-3} \text{ rad} = 0.17 \text{ degrees}$, vagyis igen kicsi.
Emberi méretskálán, vagyis néhány métertől néhány száz méterig terjedő távolságok esetén a Coriolis-hatás gyenge: egyes esetekben észrevehetetlen, máskor az effektus kísérleti kimutatásához speciális technikára van szükség.
12. Mi a helyzet nagyobb méretskálákon? Számítsd ki az $\Omega_V L/U$ arány értékét $U=10$ m/s tipikus sebesség mellett közepes földrajzi szélességen, egyre növekvő mértékű távolságokra: $L=10, 100, 1000$, illetve $10000$ km. Az arányt százalékban add meg. Mit mondhatunk az eltérülés jelentőségéről egyre növekvő méretskálák esetén?
| $L$ | $\Omega_V L/U$ | ($\Omega_V=5 \cdot 10^{-5} \text{ 1/s},\quad U=10 \text{ m/s}$) |
|---|---|---|
| 1 km | 0,5% | az eltérítő hatás nagyon gyenge |
| 10 km | 5% | az eltérítő hatás észrevehetővé válik |
| 100 km | 50% | az eltérítő hatás jelentős |
| 1000 km | 500% | az eltérítő hatás meghatározó |
Látjuk, hogy a méretskála növelésével a Coriolis-hatás egyre jelentősebb lesz.