kiszámításához meg kell határoznunk, hányféleképpen lehet M kvantumot szétosztani
N oszcillátor között. (Az ábrán az i-edik és az (i+1)-edik pálcika közötti pontok száma
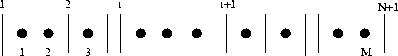
adja az i-edik oszcillátorra kiosztott kvantumok számát.) Az összes lehetséges szétosztást
úgy kapjuk meg, hogy az N-1 pálcika és az M pont (összesen N+M-1 objektum) összes permutációjából kizárjuk a pálcikák
egymás közötti és a pontok egymás közötti permutációit. Tehát
tetszőleges T-re. Behelyettesítve n(T) -t S kifejezésébe,
könnyen belátható az is, hogy 
, ha 
, azaz az entrópia pozitív minden hőmérsékleten,
tehát a kvantumok bevezetése megoldást adott az entrópia negativitásával kapcsolatos klasszikus problémákra
(lásd a 11.14 példát).