Természetesen
Jellemezzük az i-edik egységet ![]() vektorral, mely
az egység irányába mutat, és hossza a. Ekkor
vektorral, mely
az egység irányába mutat, és hossza a. Ekkor ![]()
Természetesen ![]() . Az
. Az ![]() meghatározásakor vegyük figyelembe, hogy minden
meghatározásakor vegyük figyelembe, hogy minden ![]() érték egyformán valószínű ,
érték egyformán valószínű ,
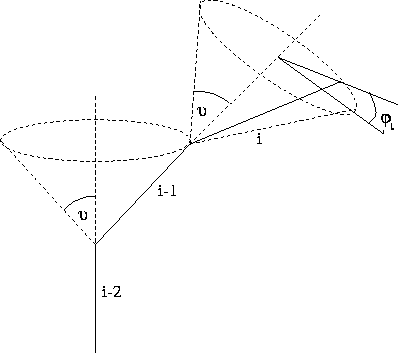
ezért az (i+2)-edik elem (i+1)-edikre merőleges
vetületének átlaga zérus, a párhuzamos vetülete
viszont ![]() . Ennek az i-edikre vett vetülete
pedig
. Ennek az i-edikre vett vetülete
pedig ![]() . Így
. Így ![]()
és általában
![]()
Ezért ![]()
ahol ![]() . Vezessük be az l = j - i
összegző indexet. Mivel
. Vezessük be az l = j - i
összegző indexet. Mivel ![]() a fenti összegben (N - l)
-szer fordul elő , írhatjuk, hogy
a fenti összegben (N - l)
-szer fordul elő , írhatjuk, hogy ![]()
Ezt kliértékelve, az N-ben vezető rendű\
járulék ![]()
ami ugyanakkora, mint az ![]() hosszúságú elemekből álló szabadon
forgó lánc átlagos négyzetes végtávolsága.
hosszúságú elemekből álló szabadon
forgó lánc átlagos négyzetes végtávolsága.
Megjegyezzük, hogy ez a feladat analóg a 11.6 példában tárgyalt "tehetetlenségi" bolyongással.