és harmonikus oszcillátorra
Az
Ezt az eredményt kapjuk az ekvipartíciótétel alapján is.
Az átlagenergia az állapotösszegből számolható ki:
![]()
és harmonikus oszcillátorra
![]()
Az ![]() határesetben
határesetben ![]() , és ebből
, és ebből
![]()
Ezt az eredményt kapjuk az ekvipartíciótétel alapján is.
Ha az energiaspektrum ![]() és a multiplicitás
és a multiplicitás ![]() , akkor
, akkor
![]()
Az ![]() esetben a fenti összeg
esetben a fenti összeg ![]() valamilyen hatványa szerint divergál. Ezt a hatványviselkedést úgy is
valamilyen hatványa szerint divergál. Ezt a hatványviselkedést úgy is
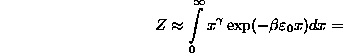
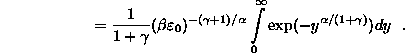
Így
![]()
![]()
Milyen egydimenziós klasszikus rendszernek felel ez meg? Ha a potenciális energia az x homogén függvénye, ![]() , akkor a viriáltétel sz
'es áll fenn (lásd Landau - Lifsic: Mechanika 10. fejezet)
, akkor a viriáltétel sz
'es áll fenn (lásd Landau - Lifsic: Mechanika 10. fejezet)
![]()
és így
![]()
Felhasználva azt, hogy a kinetikus energiára kT/2 energia jut,
![]()
Mivel egydimenziós feladatnál a spektrum nem degenerált, ezért ![]() , és így a két eredmény összehasonlításából azt kapjuk, hogy a
, és így a két eredmény összehasonlításából azt kapjuk, hogy a ![]() potenciálba
potenciálba