What is chaos?
An experiment- and observation based introduction into chaotic phenomena
Interactive material for secondary school students to be used in assisted or online teaching
Questions and tasks are set in blue boxes,
excercises and problems in yellow boxes.
I. Warming-up
A. Mixing paints of different colors is an every-day life experience:
After a few movements of stirring, intriguing filamentary patterns evolve. Further similar examples can be seen when milk is mixed in coffee, or cocoa in cakes.
Can you determine from such photographs the initial pattern before stirring?
B. Watch this picture:
Knowing that it is a long-exposure photograph taken of a motion, could you guess what moving object the green led is fixed to?
Remember, from the trajectories discussed in the standard physics curriculum you can always figure out what motions they belong to.
What you'll learn? The questions above might appear to be unconventional, and the answers you tried to give are perhaps unusual or thought-provoking. The reason: these questions touch the essence of chaos. If you are interested to become acquainted with this peculiar, but rather general, phenomenon, we invite you to an exciting journey to discover the 4 main features of Chaos. By the end of this excursion, organized about question B, you shall have a fairly complete first understanding of what modern science calls chaos. The last section of the material illustrates, by elaborating on the subject of mixing, in related to question A, that we often come across with chaotic phenomena on different scales in our every-day life, and this is just one of many possible examples.
II. Exploring the main properties of chaos
Let us start exploring the 4 main features of chaos. At the end of each module you can check your understanding by filling out a quiz,
marked with an 
. Solvers getting most questions right are rewarded
with a smiley face.
1. Temporal irregularity
You will understand that the scientific term: chaos refers to motions, but one
does not find any regularity in such motions:
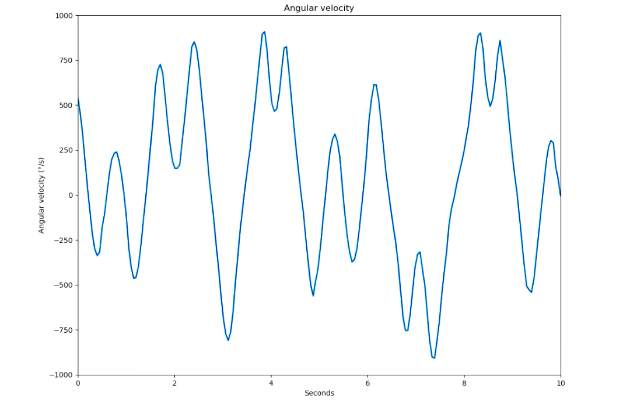Although irregular, chaos can occur in surprisingly simple systems.
Chaotic motion does not repeat itself in spite of its long duration.
2. Unpredict-
ability
When two chaotic motions start from practically the same initial condition, they tend to strongly deviate after a relatively short time. This property of chaos is expressed in everyday language as “butterfly effect”. In more scientific terms this is called the sensitivity to initial conditions. Since initially nearby motions become strongly different soon, such motions cannot be predicted on the long run.
3. Stuctured patterns in appropriate views
You will recognize that chaos, when sampled appropriately, exhibits a stuctured patterm. The permitted instantaneous states of a chaotic system are represented by a set of points arranged in an intricate way on a plane but much more points are forbidden. The permitted states trace out filaments which, alltogether, follow the rules of a special geometry, those of fractals.
4. Predictability
in terms of probabilities
You will learn that in spite of the impossibility of the long-term prediction of individual time histories, the probabilities with which the permitted states can occur can be given. One can determine the likelihood of finding a given sate during a long observation of the system. The plethora of all possible chaotic outcomes is thus fully predictable in a probabilistic view.
III. Relaxation: An application: mixing of dyes, spreading of pollutants
Looking back to point A and the photographs seen there, you might realize that stirring and mixing are chaotic processes. The fact that the initial state cannot be traced back from long time observations is a sign of unpredictability, and the filamentary patterns exhibit fractal features, indeed.
Further examples with fringerprints of stirring processes are ceramics1, ceramics2 and even abstract artistic paintings. You can read more on aesthetic aspects in chaos teaching here.
Surprisingly, similar patterns can also be seen on satellite images on continental scales (here drift ice along the coast of Kamchatka from NASA archive: http://eol.jsc.nasa.gov/scripts/sseop/photo.pl?mission=STS04&roll=79&frame=N )
Clearly, both the dye patterns and the forms in which material in our environment is advected are related to chaotic processes. A particularly worrisome case is the spreading of pollutants.
When looking at a simulation like this, the vortices can be not only stirrers in a house-hold mixer, but also oceanic or atmospheric eddies. The initially small black loop can thus represent for example both a region of high alcoholic content and a patch of concentrated pollution. The fact that this small loop becomes stretched and folded very rapidly and extends, in a filamentary, fractal-like pattern, farther than the distance of the stirrers, is a clear demonstration of the sensitive dependence on initial conditions (butterfly effect). From the point of view of our house-hold applications, chaos is an advantageous property, ensuring proper mixing, a property utilized in dough kneading. The same mechanism, however, is disadvantageous from the point of view of environmental protection since pollution on large scales spreads very rapidly, along complicatedly folding filaments which evolve in an unpredictable way.
A second simulation shows that the advected material can cover long distances while being stretched and folded, illustrating that the pollution might travel in a chaotic way huge (perhaps geographic) distances.
If you would like to see how ash spreads after a volcanic eruption in the real, measured winds of the atmosphere,
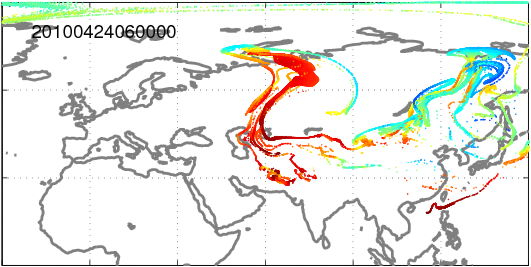
click here to download a chaos-related 'computer game' in which you can choose the location (by e.g. clikcing on an arbitrary point of the World Map) and other data of your own volcanic eruption.
Literature: T. Tél, M. Gruiz, Chaotic Dynamics, An introduction based on classical mechanics, Cambridge University Press, Cambridge, 2006
This material is dedicated to the memory of Márton Gruiz
Copyright: T. Tél, 2019-2021
This work was funded by the Content Pedagogy Research Program of the Hungarian Academy of Sciences. The technical assistance of A. Tél in setting up the pendulum experiment and carrying out the sensoric measurements is acknowledged.