From the motion on carousels to cyclones and the Gulf Stream
A guided tour full of surprises
An interactive material for secondary school students
for assisted or individual learning
Questions and tasks are set in blue boxes
excercises and problems in yellow boxes.
Problems marked with an 
are recommended for
particularly motivated readers.
Introduction
Watch the video:
What do you think of an effect like this, is it realistic?
In order to be able to answer the question above, start with a more straightforward case, video2.
You might want to carry out analogous tabletop experiments with balls on rotating platforms (e.g. an LP player or potter’s wheel). Using a web camera rotating with the platform, you can observe strange motions like in video3.
Can you decide, by comparing the last two videos, whether the platform is turning in a clockwise or in a counter-clockwise direction in video2 ?
Why, do you think, the balls follow such a curved path rather than a straight course after being tossed? You might have had similar experiences e.g., in science centers.
The videos and home experiments show that bodies released in rotating systems perform unexpected motions, deflecting from their initial course.
Do you want to know
- why demonstrations in the first video, shot at the Equator are a hoax?
- what determines the direction of the vortex observed in household plugholes?
- what causes the deflections and whirling typical of the motions of the Earth’s atmosphere and oceans?
The explanations require going beyond the high school physics syllabus. If you are ready to explore a new area,
read through the following teaching modules. Those willing to meet further challenge can also find extra information
for reading, tasks to complete and problems to solve. You will only need mathematics at a basic level: each module is
centred on one elementary relationship (a single formula in a box). At the end of each module you can check your
understanding by filling out a quiz, marked with an 
.
Solvers getting most questions right are rewarded with a smiley face.
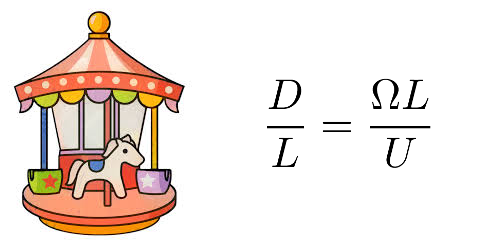
I. The basic effect: deflection of moving bodies
You will learn that deflection always occurs on a rotating disk, and discover a relationship that expresses the magnitude of the deflection if the angular velocity of the rotation is known.
II. The rotating Earth as a carousel
You will recognize that the spherical shape of the rotating Earth affects the strength of the deflection, which therefore depends on geographical latitude. You will estimate the magnitude of deflection on human scales and observe that it is very small in everyday motions.
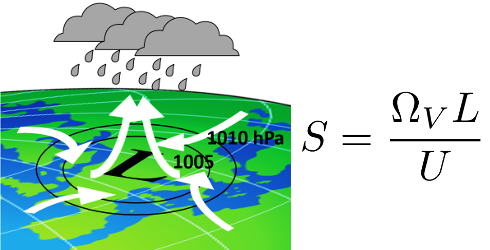
III. Strong Coriolis deflections
You will understand that in most large-scale motions nearly extending to the whole Earth (or in analogous experiments with rotating tanks) the deflection is significant, resulting in making a full turn and whirling around. You will also discover some surprising consequences.
If you do not wish to delve deeper, just continue to read the short summary below, but remember that in the background of the complexity of global atmospheric and oceanic flows there are surprising phenomena − contrary to everyday experience − such as significant deflection, which requires principles beyond the high school syllabus to explain.
Summary
The short introduction to the deflection effect (the so-called Coriolis effect) provided by sections I-III demonstrates that on the scale of objects that we are dealing in everyday life (meters to kilometers) the rotation of Earth is hardly detectable without carefully designed experiments. The Coriolis effect has the peculiar feature of becoming more significant with extension. On planetary scales (100 to 1000 kilometers) only pressure can compete with the Coriolis effect. This leads to surprising phenomena, the likes of which are never experienced in everyday life (except on carousels and in rotating tank experiments). You cannot comprehend the elements of the Earth System (let alone the great challenge of our age, climate change) without knowing about the deflection effect.
You can get an impression of the global dynamics 1) of the atmosphere and 2) of the oceans by looking at these NASA videos:
Rotational motion (deflection from straight lines) is dominant in the atmosphere, but note also that no spiraling motion, no cyclones are present at the Equator!
Swirling motion is dominant in the oceans, too, but no eddies are present at the Equator! These videos illustrate that there is no deflection effect at the Equator at all, thus you can conclude that the very frist video was based on cheating. If you watch it again, you can also observe that this deceptive video was shot without even paying attention to have the water rotate in the direction to be expected far away from the Equator on the respective hemispheres. In the case of clockwise rotation, that is, in the south, a leftward Coriolis deflection should occur in reality, as demonstrated by the motion of the balls in video2. Thus the water in the bowl should be whirling clockwise, but the performance shows a counter-clockwise rotation.
Copyright: A. Gróf, Á. Szeidemann, T. Tél
This study was funded by the Content Pedagogy Research Program of the Hungarian Academy of Sciences.